Let ω : = ∑ k ∈ Z δ k \omega : = \sum_{k\in \mathbb{Z}}\delta_k ω := ∑ k ∈ Z δ k
(1) f ω = ∑ k ∈ Z f ( k ) δ k f\omega = \sum_{k\in \mathbb{Z}}f(k)\delta_k f ω = ∑ k ∈ Z f ( k ) δ k
(2) f ∗ ω ( x ) = ∑ k ∈ Z f ( x − k ) f*\omega(x) = \sum_{k\in \mathbb{Z}}f(x - k) f ∗ ω ( x ) = ∑ k ∈ Z f ( x − k )
In other words, multiplication with ω corresponds to a sample of f f f
Theorem. The following are equivalent:
(1) F ω = ω \mathcal F\omega = \omega F ω = ω
(2) ∑ k ∈ Z F f ( k ) = ∑ k ∈ Z f ( k ) \sum_{k\in \mathbb{Z}}\mathcal Ff(k) = \sum_{k\in \mathbb{Z}}f(k) ∑ k ∈ Z F f ( k ) = ∑ k ∈ Z f ( k )
(3) ∑ k ∈ Z F f ( k + x ) = ∑ k ∈ Z f ( k ) e − 2 π i k x \sum_{k\in \mathbb{Z}}\mathcal Ff(k+x) = \sum_{k\in \mathbb{Z}}f(k)e^{-2\pi i k x} ∑ k ∈ Z F f ( k + x ) = ∑ k ∈ Z f ( k ) e − 2 πik x
Proof.
( 1 ) ⟺ ( 2 ) (1)\iff (2) ( 1 ) ⟺ ( 2 )
( F ω , f ) = ( ω , F f ) = ∑ k ∈ Z F f ( k ) (\mathcal F \omega, f) = (\omega, \mathcal Ff) = \sum_{k\in \mathbb{Z}}\mathcal Ff(k) ( F ω , f ) = ( ω , F f ) = ∑ k ∈ Z F f ( k )
On the other hand, ( ω , f ) = ∑ k ∈ Z f ( n ) (\omega,f) = \sum_{k\in \mathbb{Z}}f(n) ( ω , f ) = ∑ k ∈ Z f ( n )
Equality of right hand side is (2), and equality of left hand side is (1).
( 3 ) ⟹ ( 2 ) (3)\implies (2) ( 3 ) ⟹ ( 2 ) x = 0 x = 0 x = 0
( 1 ) ⟹ ( 3 ) : (1)\implies (3): ( 1 ) ⟹ ( 3 ) : = ( ω , τ − x F f ) = ( τ x ω , F f ) = ( F τ x ω , f ) = ( e − 2 π i x y F ω ( y ) , f ( y ) ) = (\omega, \tau_{-x}\mathcal Ff) = (\tau_x\omega, \mathcal Ff) = (\mathcal F\tau_{x}\omega, f) = (e^{-2\pi i x y}\mathcal F\omega(y),f(y)) = ( ω , τ − x F f ) = ( τ x ω , F f ) = ( F τ x ω , f ) = ( e − 2 πi x y F ω ( y ) , f ( y ))
By ( 1 ) (1) ( 1 ) ( e − 2 π i x y ω ( y ) , f ( y ) ) = ( ω ( y ) , e − 2 π i x y f ( y ) ) = ∑ k ∈ Z f ( k ) e − 2 π i k x (e^{-2\pi i xy}\omega(y),f(y)) = (\omega(y),e^{-2\pi i xy}f(y)) = \sum_{k\in \mathbb{Z}}f(k)e^{-2\pi i kx} ( e − 2 πi x y ω ( y ) , f ( y )) = ( ω ( y ) , e − 2 πi x y f ( y )) = ∑ k ∈ Z f ( k ) e − 2 πik x
Sampling theorem ¶ When we take a sample of f f f f f f 1 p \frac{1}{p} p 1 p p p
Let ω p : = ∑ k ∈ Z δ k p \omega_p: = \sum_{k \in \mathbb{Z}}\delta_{kp} ω p := ∑ k ∈ Z δ k p
Properties of
δ p \delta_p δ p and
ω p \omega_p ω p τ a δ p = δ a + p \tau_a \delta _p = \delta_{a+p} τ a δ p = δ a + p σ a δ p = 1 a δ p a \sigma_a \delta_p = \frac{1}{a}\delta_{\frac{p}{a}} σ a δ p = a 1 δ a p p > 0 , a > 0 p>0, a>0 p > 0 , a > 0 σ a ω p = 1 a ω p a \sigma_{a}\omega_p = \frac{1}{a}\omega_{\frac{p}{a}} σ a ω p = a 1 ω a p σ p ω = 1 p ω 1 p \sigma_p\omega = \frac{1}{p}\omega_{\frac{1}{p}} σ p ω = p 1 ω p 1 ω p = 1 p σ 1 p ω \omega_{p} = \frac{1}{p}\sigma_{\frac{1}{p}}\omega ω p = p 1 σ p 1 ω Consequently,
F ω p = F ( 1 p σ 1 p ω ) = 1 p ⋅ p σ p F ω = σ p ω = 1 p ω 1 p . \mathcal F \omega_p = \mathcal F(\frac{1}{p}\sigma_{\frac{1}{p}}\omega) = \frac{1}{p}\cdot p\sigma_p\mathcal F\omega = \sigma_p\omega = \frac{1}{p}\omega_{\frac{1}{p}}. F ω p = F ( p 1 σ p 1 ω ) = p 1 ⋅ p σ p F ω = σ p ω = p 1 ω p 1 . Also, since ω p − = ω p \omega_p^{-} = \omega_p ω p − = ω p F − 1 ω p = F ω p − = 1 p ω 1 p \mathcal F^{-1}\omega_p = \mathcal F\omega_p^{-} = \frac{1}{p}\omega_{\frac{1}{p}} F − 1 ω p = F ω p − = p 1 ω p 1
Sampling of bandlimited signals ¶ Let f ∈ S f\in \mathcal S f ∈ S F f \mathcal Ff F f [ − p 2 , p 2 ] [-\frac{p}{2},\frac{p}{2}] [ − 2 p , 2 p ] F f ∗ ω p \mathcal F f*\omega_p F f ∗ ω p Π p \mathcal \Pi_p Π p
( F f ∗ ω p ) ⋅ Π p = F f . (\mathcal Ff*\omega_p)\cdot \Pi_p = \mathcal Ff. ( F f ∗ ω p ) ⋅ Π p = F f . Then taking Fourier inversion both side, applying the convolution theorem, we get
F − 1 L H S = F − 1 ( F f ∗ ω p ) ∗ F − 1 Π p = ( f ⋅ F − 1 ω p ) ∗ p s i n c ( p x ) = ( f ⋅ 1 p ω 1 p ) ∗ p s i n c ( p x ) = ∑ k ∈ Z f ( k p ) δ k p ∗ s i n c ( p x ) = ∑ k ∈ Z f ( k p ) τ k p s i n c ( p x ) = ∑ k ∈ Z f ( k p ) s i n c ( p ( x − k p ) ) = F − 1 R H S = f ( x ) \begin{split}
\mathcal F^{-1}LHS &= \mathcal F^{-1}(\mathcal Ff *\omega_p)* \mathcal F^{-1}\Pi_p \\
& = (f\cdot \mathcal F^{-1}\omega_p)*p\mathrm{sinc}(px)\\
& = (f\cdot \frac{1}{p}\omega_{\frac{1}{p}})*p \mathrm{sinc}(px)\\
& = \sum_{k\in \mathbb{Z}}f(\frac{k}{p})\delta_{\frac{k}{p}}*\mathrm{sinc}(px) \\
&=\sum_{k\in \mathbb{Z}}f(\frac{k}{p})\tau_{\frac{k}{p}}\mathrm{sinc}(px) \\
& = \sum_{k\in \mathbb{Z}}f(\frac{k}{p})\mathrm{sinc}(p(x - \frac{k}{p}))\\
& = \mathcal F^{-1}RHS\\
& = f(x)
\end{split} F − 1 L H S = F − 1 ( F f ∗ ω p ) ∗ F − 1 Π p = ( f ⋅ F − 1 ω p ) ∗ p sinc ( p x ) = ( f ⋅ p 1 ω p 1 ) ∗ p sinc ( p x ) = k ∈ Z ∑ f ( p k ) δ p k ∗ sinc ( p x ) = k ∈ Z ∑ f ( p k ) τ p k sinc ( p x ) = k ∈ Z ∑ f ( p k ) sinc ( p ( x − p k )) = F − 1 R H S = f ( x ) Let f f f s u p p ( F f ) ⊂ [ − p 2 , p 2 ] supp(\mathcal Ff)\subset[-\frac{p}{2},\frac{p}{2}] s u pp ( F f ) ⊂ [ − 2 p , 2 p ] f ( x ) = ∑ k ∈ Z f ( k p ) s i n c ( p x − k ) f(x) = \sum_{k\in \mathbb{Z}}f(\frac{k}{p})\mathrm{sinc}(px - k) f ( x ) = ∑ k ∈ Z f ( p k ) sinc ( p x − k )
Periodic distributions ¶ Let T ∈ D ′ T\in \mathcal D' T ∈ D ′ T T T 1-periodic provided that τ 1 T = T \tau_1 T = T τ 1 T = T
Lemma ¶ A periodic distribution is tempered.
Proof. To show T T T ( T , g ) (T,g) ( T , g ) g ∈ S g\in \mathcal S g ∈ S T T T T T T
Let φ ( x ) = j ( x ) ∑ k ∈ Z j ( x − k ) \varphi(x) = \frac{j(x)}{\sum_{k\in \mathbb{Z}}j(x - k)} φ ( x ) = ∑ k ∈ Z j ( x − k ) j ( x ) φ n ( x ) = φ ( x − n ) \varphi_n(x) = \varphi(x - n) φ n ( x ) = φ ( x − n ) ( φ n ) n ∈ Z (\varphi_{n})_{n \in \mathbb Z} ( φ n ) n ∈ Z
(1) φ n ∈ C c ∞ ( n − 1 , n + 1 ) \varphi_n \in \mathscr{C}_c^{\infty}(n-1,n+1) φ n ∈ C c ∞ ( n − 1 , n + 1 )
(2) ∑ n ∈ Z φ n ( x ) = 1 \sum_{n\in \mathbb{Z}}\varphi_n(x) = 1 ∑ n ∈ Z φ n ( x ) = 1 x ∈ R x\in \mathbb{R} x ∈ R
The above follows from observing ∑ n ∈ Z j ( x − n ) = j ( x − m ) + j ( x − ( m + 1 ) ) + j ( x − ( m − 1 ) ) \sum_{n\in \mathbb{Z}}j(x-n) = j(x-m)+j(x-(m+1))+j(x-(m-1)) ∑ n ∈ Z j ( x − n ) = j ( x − m ) + j ( x − ( m + 1 )) + j ( x − ( m − 1 )) m m m − 1 ≤ x − m ≤ 1 -1\leq x-m\leq 1 − 1 ≤ x − m ≤ 1
φ n \varphi_n φ n partition of unity subordinate to the open cover ⋃ n ∈ Z ( n − 1 , n + 1 ) \bigcup_{n\in \mathbb{Z}}(n-1,n+1) ⋃ n ∈ Z ( n − 1 , n + 1 ) R \mathbb{R} R
Then ( T , g ) = ( T , g ( x ) ⋅ 1 ) = ( T , g ( x ) ⋅ ∑ n ∈ Z φ n ( x ) ) = ∑ n ∈ Z ( T , g φ n ) (T,g) = (T,g(x)\cdot 1) = (T,g(x)\cdot \sum_{n\in \mathbb{Z}}\varphi_n(x)) = \sum_{n\in \mathbb{Z}}(T,g\varphi_n) ( T , g ) = ( T , g ( x ) ⋅ 1 ) = ( T , g ( x ) ⋅ ∑ n ∈ Z φ n ( x )) = ∑ n ∈ Z ( T , g φ n )
Since T T T ( T , g φ n ) = ( τ n T , g φ n ) = ( T , τ − n ( g φ n ) ) = ( T , g ( x + n ) φ n ( x + n ) ) = ( T , φ 0 τ − n g ) (T,g\varphi_n) = (\tau_n T, g\varphi_n) = (T,\tau_{-n}(g\varphi_n)) = (T,g(x+n)\varphi_n(x + n)) = (T,\varphi_0 \tau_{-n}g) ( T , g φ n ) = ( τ n T , g φ n ) = ( T , τ − n ( g φ n )) = ( T , g ( x + n ) φ n ( x + n )) = ( T , φ 0 τ − n g ) φ 0 = φ \varphi_0 = \varphi φ 0 = φ φ 0 ( x ) g ( x + n ) \varphi_0(x)g(x+n) φ 0 ( x ) g ( x + n ) [ − 1 , 1 ] [-1,1] [ − 1 , 1 ]
Since T T T T T T N N N C ∞ [ − 1 , 1 ] \mathscr{C}^{\infty}[-1,1] C ∞ [ − 1 , 1 ] K = [ − 1 , 1 ] K = [-1,1] K = [ − 1 , 1 ] C > 0 C>0 C > 0 N N N ∣ ( T , ψ ) ∣ ≤ C ∑ 0 ≤ l ≤ N sup x ∈ [ − 1 , 1 ] ∣ ψ ( l ) ( x ) ∣ |(T,\psi)|\leq C \sum_{0\leq l \leq N}\sup_{x \in [-1,1]}|\psi^{(l)}(x)| ∣ ( T , ψ ) ∣ ≤ C ∑ 0 ≤ l ≤ N sup x ∈ [ − 1 , 1 ] ∣ ψ ( l ) ( x ) ∣ ψ ( x ) = φ 0 ( x ) g ( x + n ) \psi(x) = \varphi_0(x)g(x+n) ψ ( x ) = φ 0 ( x ) g ( x + n )
∣ ( T , φ 0 ( x ) g ( x + n ) ) ∣ ≤ C ′ ⋅ ∑ 0 ≤ l ≤ N sup x ∈ [ − 1 , 1 ] ∣ φ 0 ( l ) ( x ) ∣ ⋅ ∑ 0 ≤ l ≤ N sup x ∈ [ n − 1 , n + 1 ] ∣ g ( l ) ( x ) ∣ ≤ C ′ ⋅ ∑ 0 ≤ l ≤ N sup x ∈ [ − 1 , 1 ] ∣ φ 0 ( l ) ( x ) ∣ ⋅ ∑ 0 ≤ l ≤ N sup x ∈ [ n − 1 , n + 1 ] ∣ ( 1 + x 2 ) g ( l ) ( x ) 1 1 + x 2 ∣ ≤ C ′ ⋅ ∑ 0 ≤ l ≤ N sup x ∈ [ − 1 , 1 ] ∣ φ 0 ( l ) ( x ) ∣ ⋅ 1 1 + ( ∣ n ∣ − 1 ) 2 ∑ 0 ≤ l ≤ N ∥ g ∥ ( 2 , l ) . \begin{split}
|(T,\varphi_0(x)g(x+n))|&\leq C' \cdot \sum_{0\leq l \leq N}\sup_{x\in [-1,1]}|\varphi_0^{(l)}(x)| \cdot \sum_{0\leq l \leq N}\sup_{x\in [n-1,n+1]}|g^{(l)}(x)| \\
&\leq C' \cdot \sum_{0\leq l \leq N}\sup_{x\in [-1,1]}|\varphi_0^{(l)}(x)| \cdot \sum_{0\leq l \leq N}\sup_{x \in [n-1,n+1]} |(1+x^2)g^{(l)}(x)\frac{1}{1+x^2}|\\
&\leq C' \cdot \sum_{0\leq l \leq N}\sup_{x\in [-1,1]}|\varphi_0^{(l)}(x)| \cdot \frac{1}{1+(|n|-1)^2}\sum_{0\leq l \leq N}\|g\|_{(2,l)}.
\end{split} ∣ ( T , φ 0 ( x ) g ( x + n )) ∣ ≤ C ′ ⋅ 0 ≤ l ≤ N ∑ x ∈ [ − 1 , 1 ] sup ∣ φ 0 ( l ) ( x ) ∣ ⋅ 0 ≤ l ≤ N ∑ x ∈ [ n − 1 , n + 1 ] sup ∣ g ( l ) ( x ) ∣ ≤ C ′ ⋅ 0 ≤ l ≤ N ∑ x ∈ [ − 1 , 1 ] sup ∣ φ 0 ( l ) ( x ) ∣ ⋅ 0 ≤ l ≤ N ∑ x ∈ [ n − 1 , n + 1 ] sup ∣ ( 1 + x 2 ) g ( l ) ( x ) 1 + x 2 1 ∣ ≤ C ′ ⋅ 0 ≤ l ≤ N ∑ x ∈ [ − 1 , 1 ] sup ∣ φ 0 ( l ) ( x ) ∣ ⋅ 1 + ( ∣ n ∣ − 1 ) 2 1 0 ≤ l ≤ N ∑ ∥ g ∥ ( 2 , l ) . This shows ∣ ( T , g ) ∣ ≤ C ′ ⋅ ∑ 0 ≤ l ≤ N sup x ∈ [ − 1 , 1 ] ∣ φ 0 ( l ) ( x ) ∣ ⋅ ∑ n ∈ Z 1 1 + ( ∣ n ∣ − 1 ) 2 ⋅ ∑ 0 ≤ k , l ≤ N ∥ g ∥ ( k , l ) |(T,g)|\leq C'\cdot \sum_{0\leq l \leq N}\sup_{x\in [-1,1]}|\varphi_0^{(l)}(x)| \cdot \sum_{n\in \mathbb{Z}} \frac{1}{1+(|n|-1)^2} \cdot \sum_{0\leq k,l\leq N}\|g\|_{(k,l)} ∣ ( T , g ) ∣ ≤ C ′ ⋅ ∑ 0 ≤ l ≤ N sup x ∈ [ − 1 , 1 ] ∣ φ 0 ( l ) ( x ) ∣ ⋅ ∑ n ∈ Z 1 + ( ∣ n ∣ − 1 ) 2 1 ⋅ ∑ 0 ≤ k , l ≤ N ∥ g ∥ ( k , l ) T T T
Fourier expansion of periodic distribution ¶ ( F T , f ) = ( T , F f ) = ∑ n ∈ Z ( T , φ 0 ( x ) F f ( n + x ) ) = ( φ 0 T , ∑ n ∈ Z F f ( n + x ) ) = ( φ 0 T , ∑ n ∈ Z f ( n ) e − 2 π i n x ) = ∑ n ∈ Z f ( n ) ( φ 0 T , e − 2 π i n x ) = ∑ n ∈ Z T ^ ( n ) f ( n ) \begin{split}
(\mathcal FT,f) &= (T,\mathcal Ff)\\
&= \sum_{n\in \mathbb{Z}}(T,\varphi_0(x)\mathcal Ff(n+x)) \\
&= (\varphi_0 T,\sum_{n\in \mathbb{Z}}\mathcal Ff(n+x)) \\
& = (\varphi_0 T,\sum_{n \in \mathbb{Z}}f(n)e^{-2\pi i n x}) \\
& = \sum_{n \in \mathbb{Z}}f(n)(\varphi_0T,e^{-2\pi inx})\\
&= \sum_{n\in \mathbb{Z}}\hat{T}(n)f(n)
\end{split} ( F T , f ) = ( T , F f ) = n ∈ Z ∑ ( T , φ 0 ( x ) F f ( n + x )) = ( φ 0 T , n ∈ Z ∑ F f ( n + x )) = ( φ 0 T , n ∈ Z ∑ f ( n ) e − 2 πin x ) = n ∈ Z ∑ f ( n ) ( φ 0 T , e − 2 πin x ) = n ∈ Z ∑ T ^ ( n ) f ( n ) where we define T ^ ( n ) \hat{T}(n) T ^ ( n ) ( T , φ 0 ( x ) e − 2 π i n x ) (T,\varphi_0(x)e^{-2\pi i nx}) ( T , φ 0 ( x ) e − 2 πin x )
The value ( φ 0 T , e − 2 π i n x ) (\varphi_0 T,e^{-2\pi i nx}) ( φ 0 T , e − 2 πin x ) T ^ ( n ) \hat{T}(n) T ^ ( n )
Proof. Let ( ψ n ) n ∈ Z (\psi_n)_{n \in \mathbb{Z}} ( ψ n ) n ∈ Z ( φ n ) n ∈ Z (\varphi_n)_{n\in \mathbb{Z}} ( φ n ) n ∈ Z A = ( φ 0 T , e − 2 π i n x ) − ( ψ 0 T , e − 2 π i n x ) = ( ( ψ 0 − φ 0 ) T , e − 2 π i n x ) = ( T , ( φ 0 ( x ) − ψ 0 ( x ) ) e − 2 π i n x ) A = (\varphi_0 T,e^{-2\pi i n x}) - (\psi_0 T,e^{-2\pi i nx}) = ((\psi_0 - \varphi_0)T,e^{-2\pi i nx}) = (T,(\varphi_0(x) - \psi_0(x))e^{-2\pi i nx}) A = ( φ 0 T , e − 2 πin x ) − ( ψ 0 T , e − 2 πin x ) = (( ψ 0 − φ 0 ) T , e − 2 πin x ) = ( T , ( φ 0 ( x ) − ψ 0 ( x )) e − 2 πin x )
( N + 1 ) A = ∑ ∣ n ∣ ≤ N ( τ n T , ( φ 0 ( x ) − ψ 0 ( x ) e − 2 π i n x ) = ∑ ∣ n ∣ ≤ N ( T , ( ψ n ( x ) − φ n ( x ) ) e − 2 π i n x ) = ( T , ( ∑ ∣ n ∣ ≤ N ψ n ( x ) − ∑ ∣ n ∣ ≤ N φ n ( x ) ) e − 2 π i n x ) \begin{split}
(N+1)A &= \sum_{|n|\leq N}(\tau_nT,(\varphi_0(x) - \psi_0(x)e^{-2\pi i nx})\\
&=\sum_{|n|\leq N}(T,(\psi_n(x) - \varphi_n(x))e^{-2\pi i nx})\\
& = (T,(\sum_{|n|\leq N}\psi_n(x) - \sum_{|n|\leq N}\varphi_n(x))e^{-2\pi i nx})
\end{split} ( N + 1 ) A = ∣ n ∣ ≤ N ∑ ( τ n T , ( φ 0 ( x ) − ψ 0 ( x ) e − 2 πin x ) = ∣ n ∣ ≤ N ∑ ( T , ( ψ n ( x ) − φ n ( x )) e − 2 πin x ) = ( T , ( ∣ n ∣ ≤ N ∑ ψ n ( x ) − ∣ n ∣ ≤ N ∑ φ n ( x )) e − 2 πin x ) Since both φ n \varphi_n φ n ψ n \psi_n ψ n ⋃ n ∈ Z ( n − 1 , n + 1 ) \bigcup_{n\in \mathbb{Z}}(n-1,n+1) ⋃ n ∈ Z ( n − 1 , n + 1 ) ∑ ∣ n ∣ ≤ N ( ψ n ( x ) − φ n ( x ) ) = 0 \sum_{|n|\leq N}(\psi_n(x) - \varphi_n(x)) = 0 ∑ ∣ n ∣ ≤ N ( ψ n ( x ) − φ n ( x )) = 0 [ − N , N ] [-N,N] [ − N , N ] ∑ ∣ n ∣ ≤ N ( φ n − ψ n ) e − 2 π i n x → 0 \sum_{|n|\leq N}(\varphi_n - \psi_n)e^{-2\pi i nx }\to 0 ∑ ∣ n ∣ ≤ N ( φ n − ψ n ) e − 2 πin x → 0 C c ∞ ( R ) \mathscr{C}_c^{\infty}(\mathbb{R}) C c ∞ ( R ) N → ∞ N\to \infty N → ∞ ( N + 1 ) ∣ A ∣ → 0 (N+1)|A| \to 0 ( N + 1 ) ∣ A ∣ → 0 N → ∞ N\to \infty N → ∞ A = 0 A = 0 A = 0 □ \square □
We have proved the following theorem
Fourier expansion of periodic distributions ¶ Let T ∈ D ′ T\in \mathcal D' T ∈ D ′
F T = ∑ n ∈ Z T ^ ( n ) δ n \mathcal FT = \sum_{n\in \mathbb{Z}}\hat{T}(n)\delta_n F T = ∑ n ∈ Z T ^ ( n ) δ n ( F T , f ) = ∑ n ∈ Z T ^ ( n ) f ( n ) (\mathcal FT,f) = \sum_{n\in \mathbb{Z}}\hat{T}(n)f(n) ( F T , f ) = ∑ n ∈ Z T ^ ( n ) f ( n )
T = ∑ n ∈ Z T ^ ( n ) T e 2 π i n x T = \sum_{n\in \mathbb{Z}}\hat{T}(n)T_{e^{2\pi i n x}} T = ∑ n ∈ Z T ^ ( n ) T e 2 πin x
Proof.
( T , f ) = ( F − 1 F T , f ) = ( F T , F − 1 f ) = ( ∑ n ∈ Z T ^ ( n ) δ n ( x ) , ∫ f ( y ) e 2 π i x y d y ) = ∑ n ∈ Z T ^ ( n ) ∫ − ∞ + ∞ f ( y ) e 2 π i n y d y (T,f) = (\mathcal F^{-1}\mathcal F T,f) = (\mathcal F T, \mathcal F^{-1}f) = (\sum_{n\in \mathbb{Z}}\hat{T}(n)\delta_n (x), \int f(y)e^{2\pi i x y}dy ) = \sum_{n\in \mathbb{Z}}\hat{T}(n)\int_{-\infty}^{+\infty} f(y)e^{2\pi i n y} dy ( T , f ) = ( F − 1 F T , f ) = ( F T , F − 1 f ) = ( ∑ n ∈ Z T ^ ( n ) δ n ( x ) , ∫ f ( y ) e 2 πi x y d y ) = ∑ n ∈ Z T ^ ( n ) ∫ − ∞ + ∞ f ( y ) e 2 πin y d y
When T = T g T = T_g T = T g g g g T ^ ( n ) = ∫ − ∞ + ∞ g ( x ) φ 0 ( x ) e − 2 π i n x d x = ∑ k ∈ Z ∫ k − 1 2 k + 1 2 g ( x ) φ 0 ( x ) e − 2 π i n x d x = ∑ k ∈ Z ∫ − 1 2 1 2 g ( x − k ) φ k ( x ) e − 2 π i n x d x = ∫ − 1 2 1 2 g ( x ) e − 2 π i n x ∑ k ∈ Z φ k ( x ) d x = ∫ − 1 2 1 2 g ( x ) e − 2 π i n x = g ^ ( n ) \hat{T}(n) = \int_{-\infty}^{+\infty} g(x)\varphi_0(x) e^{-2\pi i n x}dx = \sum_{k\in \mathbb{Z}}\int_{k-\frac{1}{2}}^{k+\frac{1}{2}}g(x)\varphi_0(x)e^{-2\pi i n x}dx = \sum_{k\in \mathbb{Z}}\int_{-\frac{1}{2}}^{\frac{1}{2}} g(x-k)\varphi_k(x)e^{-2\pi i n x}dx = \int_{-\frac{1}{2}}^{\frac{1}{2}} g(x)e^{-2\pi i n x}\sum_{k\in \mathbb{Z}}\varphi_k(x) dx = \int_{-\frac{1}{2}}^{\frac{1}{2}} g(x)e^{-2\pi i n x} = \hat{g}(n) T ^ ( n ) = ∫ − ∞ + ∞ g ( x ) φ 0 ( x ) e − 2 πin x d x = ∑ k ∈ Z ∫ k − 2 1 k + 2 1 g ( x ) φ 0 ( x ) e − 2 πin x d x = ∑ k ∈ Z ∫ − 2 1 2 1 g ( x − k ) φ k ( x ) e − 2 πin x d x = ∫ − 2 1 2 1 g ( x ) e − 2 πin x ∑ k ∈ Z φ k ( x ) d x = ∫ − 2 1 2 1 g ( x ) e − 2 πin x = g ^ ( n )
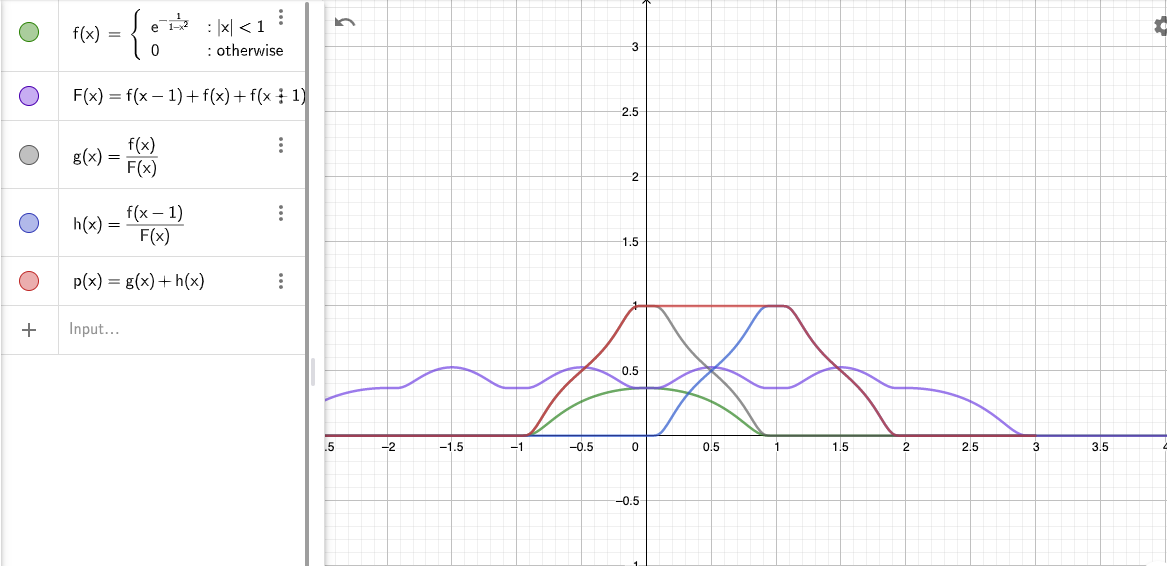
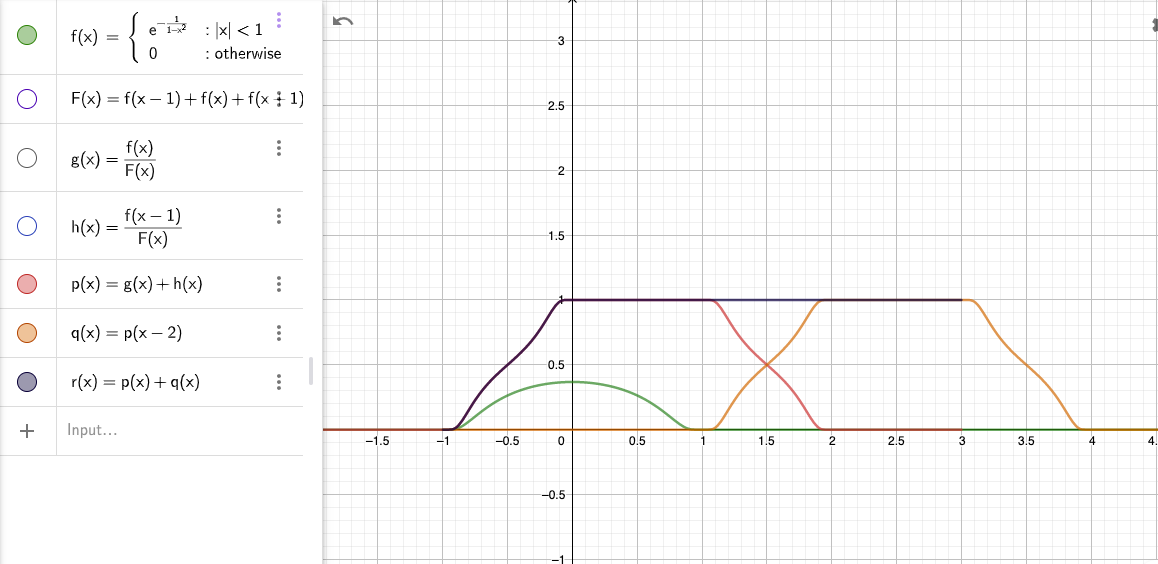
Appendix: Picture of ( φ n ) (\varphi_n) ( φ n ) ¶ In the following picture, h ( x ) h(x) h ( x ) φ 1 \varphi_1 φ 1 g ( x ) g(x) g ( x ) φ 0 \varphi_0 φ 0 p ( x ) p(x) p ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ]
Let q ( x ) q(x) q ( x ) p ( x ) p(x) p ( x ) [ 2 , 3 ] [2,3] [ 2 , 3 ] p ( x ) p(x) p ( x ) q ( x ) q(x) q ( x ) [ 0 , 3 ] [0,3] [ 0 , 3 ]